CS231n-Unsupervised Learning and Generative Models

Unsupervised Learning and Generative Models

Unsupervised Learning

Supervised Learning

• Data: (x,y) x is data, y is label
• Goal: Learn a function to map s→y
• Examples: Classification, regression, object detection, semantic segmentation, image caption, etc.

Unsupervised Learning

• Data: x,just data, no labels!
• Goal: Learn some underlying hidden structure of some data
• Examples: Clustering, Dimensionality reduction(principal Component Analysis),feature learning, density estimation,etc.

Generative Models

Given training data, geneerate new samples from same distribution.

• Explicit density
  • Tractable demsity
    • Fully Visible Belief Nets(Change of variables models(nonlinear ICA))
      • NADE
      • MADE
      • PixelRNN/CNN
    • Approximate density
      • Variational: Variational Autoencoders
      • Markov Chain: Boltzmann Machine
• Implicit density
  • Direct(GAN)
  • Markov Chain(GSN)

PixelRNN and PixelCNN

• use neural network to express this comlex distribution!
• PixelCNN与semantic Segmentation的区别：一个是直接使用原始图片的像素值，一个是使用人工标注的语义分割图片

Variational Autoencoders(VAE)

这里视频讲的不是很清楚，推荐苏老师的博客

在讨论VAE之前，我们先来看一看Autoencoders

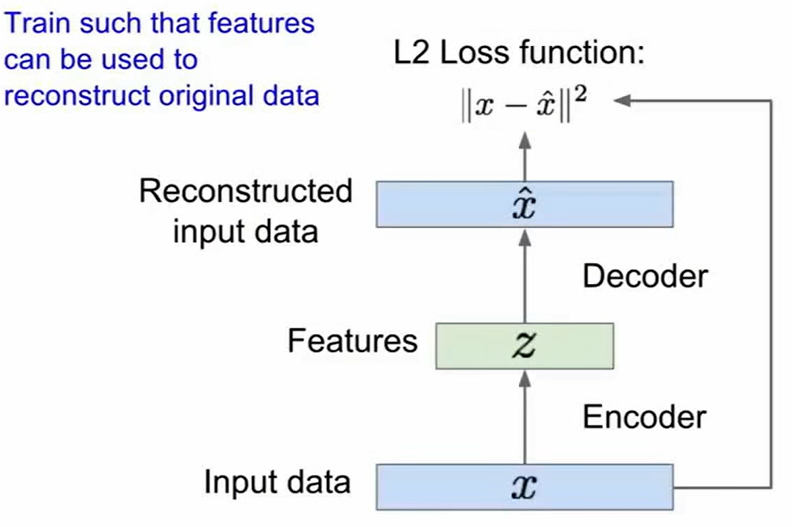
在学习之前先使用Autoencoders，可以减少features的数量，从而减少过拟合的风险

• AE可以起到降维的作用，但是它不能产生新的采样以达到增加样本的作用

  • 在样本量不足的场景当中，我们想要增加样本量以达到更好的效果。如果能够根据一批一批数据样本${X_1,…,X_n}$直接找到$X$的分布$p(X)$,那我直接根据$p(X)$来采样就可以了。但是这是不能实现的。
  • 于是我们曲线救国，把AE中的向量z（确定的）改为一个正态分布（不确定的）这样我们就把有限的数据样本扩展到无穷维了（应为正态分布里面可以随便采样）（使用正态分布是启发式的）

  

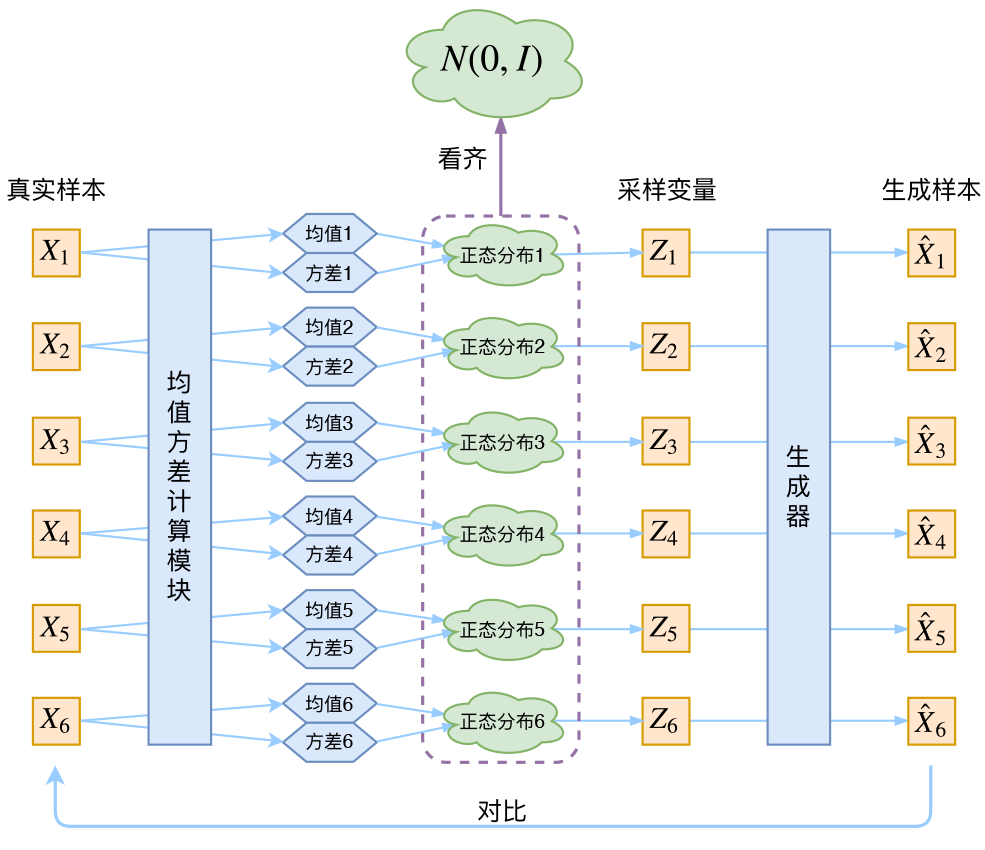
• 其中均值方差计算模块与生成器模块都是由网络实现的（什么不好算就交给网络，这是神经网络时代的哲学）

Generative Adversarial Networks(GAN)

当样本的分布过于复杂之时，我们可以放弃考虑样本分布，转而使用一个博弈的思想，一个Generator network，和一个Discriminator network，生成网络尝试去欺骗过判别网络，判别网络尝试去区分出真与假的照片。

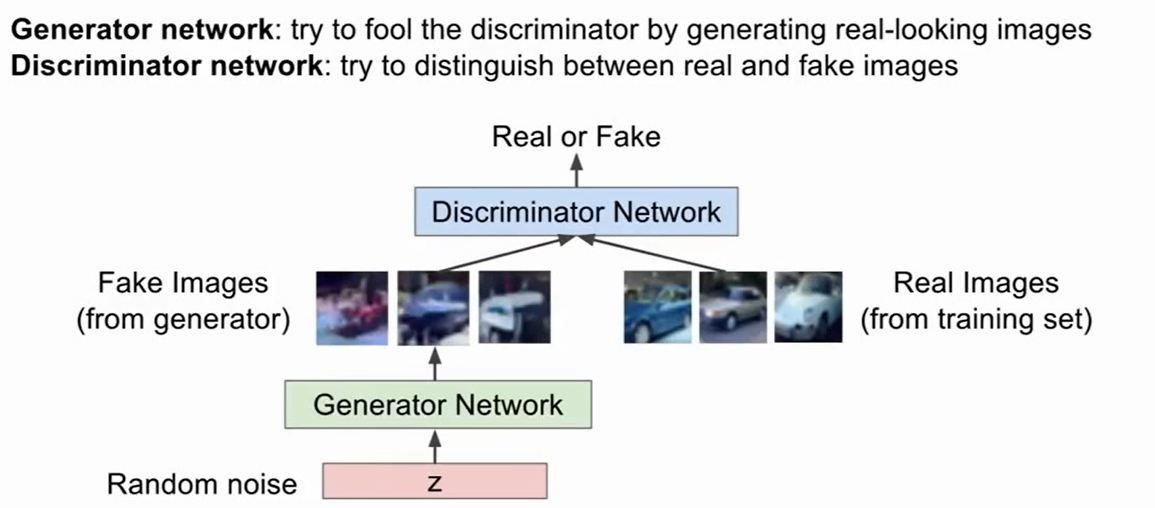
我们最小化下面这个函数

$$
\min_{\theta_g}\max_{\theta_g}[E_{x-p_{data}}\log D_{\theta_d}(x)+E_{z-p(z)}\log (1-D_{\theta_d}(G_{\theta_g}(z)))]
$$

步骤：

1. Gradient Ascent on discriminator

   $$
   \max_{\theta_g}[E_{x-p_{data}}\log D_{\theta_d}(x)+E_{z-p(z)}\log (1-D_{\theta_d}(G_{\theta_g}(z)))]
   $$

2. Gradient descent on generator

   $$
   \min_{\theta_g}E_{z-p(z)}\log (1-D_{\theta_d}(G_{\theta_g}(z)))
   $$

但是对于生成器的目标函数，注意到它在生成质量不好时梯度较小，生成质量较小时梯度较大，这是我们不希望的，网络收敛速度很慢，于是我们转而最大化下面这个函数：

$$
\max_{\theta_g}E_{z-p(z)}\log D_{\theta_d}(G_{\theta_g}(z))
$$