约 3606 个字 10 行代码 4 张图片 预计阅读时间 18 分钟 共被读过 次
第1章强化学习基础总结¶
1.1 强化学习概述¶
核心定义¶
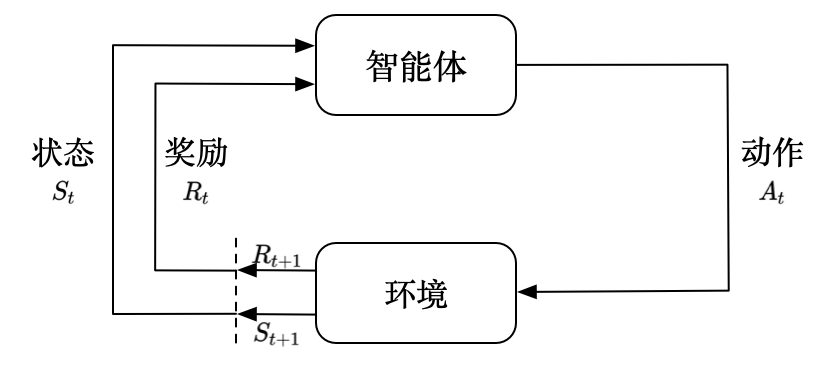
- 强化学习(RL):智能体通过与环境交互最大化累积奖励的学习范式。
- 基本组成:智能体(Agent)与环境(Environment)持续交互,输出动作(Action)并接收状态(State)和奖励(Reward)。
强化学习 vs 监督学习¶
| 对比维度 | 监督学习 | 强化学习 |
|---|---|---|
| 数据特性 | 独立同分布(i.i.d.) | 时间序列数据(关联性强) |
| 反馈方式 | 即时标签反馈 | 延迟奖励信号 |
| 目标 | 拟合标注数据 | 最大化长期奖励 |
| 探索-利用 | 无 | 需平衡探索新动作与利用已知动作 |
标准强化学习 vs 深度强化学习¶
- 标准强化学习:比如 TD-Gammon 玩 Backgammon 游戏的过程,其实就是设计特征,然后训练价值函数的过程,如下图所示。标准强化学习先设计很多特征,这些特征可以描述现在整个状态。得到这些特征后,我们就可以通过训练一个分类网络或者分别训练一个价值估计函数来采取动作。
- 深度强化学习:自从我们有了深度学习,有了神经网络,就可以把智能体玩游戏的过程改进成一个端到端训练(end-to-end training)的过程,如下图所示。我们不需要设计特征,直接输入状态就可以输出动作。我们可以用一个神经网络来拟合价值函数或策略网络,省去特征工程(feature engineering)的过程。

关键概念¶
- 延迟奖励:动作的长期影响需通过多步交互体现(如雅达利游戏最终得分)。
- 探索与利用:探索尝试新动作可能获得更高奖励,利用执行已知最优动作。
- 马尔可夫决策过程(MDP):完全可观测环境下的数学建模框架。
- 部分可观测马尔可夫决策过程(POMDP):智能体仅能获取部分环境状态信息。
应用实例¶
- AlphaGo:超越人类棋手的深度强化学习模型。
- 机械臂控制Deep Learning for Robots: Learning from Large-Scale Interaction:通过虚拟环境训练后迁移到真实机器人。
- 游戏AI:如雅达利Pong游戏,智能体通过试错学习策略。
1.2 序列决策¶
核心流程¶
- 交互循环:智能体根据当前状态选择动作,环境返回新状态和奖励。
- 公式:\(H_t = o_1, a_1, r_1, \ldots, o_t, a_t, r_t\) - 状态与观测:
- 状态(State) \(S_t\) :环境的完整描述。整个游戏的状态看成关于历史的函数
- 观测(Observation) \(O_t\) :状态的部分信息(可能不完整)。
- 环境状态有自己的函数 \(s_{t}^e=f^e(H_{t)})\) 来更新状态
- agent状态有自己的函数 \(s_{t}^a=f^a(H_{t)})\) 来更新状态
- 当智能体的状态与环境的状态等价的时候,即当智能体能够观察到环境的所有状态时,我们称这个环境是完全可观测的(fully observed)。在这种情况下面,强化学习通常被建模成一个马尔可夫决策过程 (Markov decision process,MDP)的问题。在马尔可夫决策过程中,
- 当智能体只能看到部分的观测,我们就称这个环境是部分可观测的(partially observed)。在这种情况下,强化学习通常被建模成部分可观测马尔可夫决策过程(partially observable Markov decision process, POMDP) 的问题。部分可观测马尔可夫决策过程是马尔可夫决策过程的一种泛化。部分可观测马尔可夫决策过程依然具有马尔可夫性质,但是假设智能体无法感知环境的状态,只能知道部分观测值。比如在自动驾驶中,智能体只能感知传感器采集的有限的环境信息。部分可观测马尔可夫决策过程可以用一个七元组描述:
$$
(S,A,T,R,Ω,O,γ)
$$
其中:
- \(S\) 表示状态空间,为隐变量,
- \(A\) 为动作空间,
- \(T(s′∣s,a)\) 为状态转移概率,
- \(R\) 为奖励函数,
- \(Ω(o∣s,a)\) 为观测概率,
- \(O\) 为观测空间,
- \(γ\) 为折扣系数。
- [[POMDP的一些参数说明]]
奖励设计¶
- 奖励信号:标量值反馈,衡量动作的短期效果。
- 长期目标:最大化期望累积奖励 \(G_t = \sum_{k=0}^\infty \gamma^k r_{t+k+1}\),其中 \(\gamma\) 为折扣因子。
1.3 动作空间¶
- 离散动作空间:有限个可选动作(如围棋的落子位置)。
- 连续动作空间:动作值为实数向量(如机器人关节角度控制)。
1.4 强化学习智能体的组成¶
三大核心组件¶
- 策略(Policy):
- 随机策略:\(\pi(a|s)\) 输出动作概率分布。
- 确定策略:直接选择最优动作 \(a^* = \arg\max_a \pi(a|s)\)。 - 价值函数(Value Function):
- 状态价值函数: \(V_\pi(s) = \mathbb{E}_\pi[G_t | s_t = s]=\mathbb{E}_{\pi}\left[ \sum^{\infty}_{{k=0}}\gamma^kr_{t+k+1}|s_{t}=s \right]\) 。
- 动作价值函数(Q函数): \(Q_\pi(s,a) = \mathbb{E}_\pi[G_t | s_t = s, a_t = a]=\mathbb{E}_{\pi}\left[ \sum^{\infty}_{{k=0}}\gamma^kr_{t+k+1}|s_{t}=s,a_{t}=a \right]\) 。 - 模型(Model):
- 状态转移概率: \(p^a_{ss'}=p(s_{t+1}=s'|s_{t}=s,a_{t}=a)\) 。
- 奖励函数:\(R(s,a) = \mathbb{E}[r_{t+1} | s_t = s, a_t = a]\)。
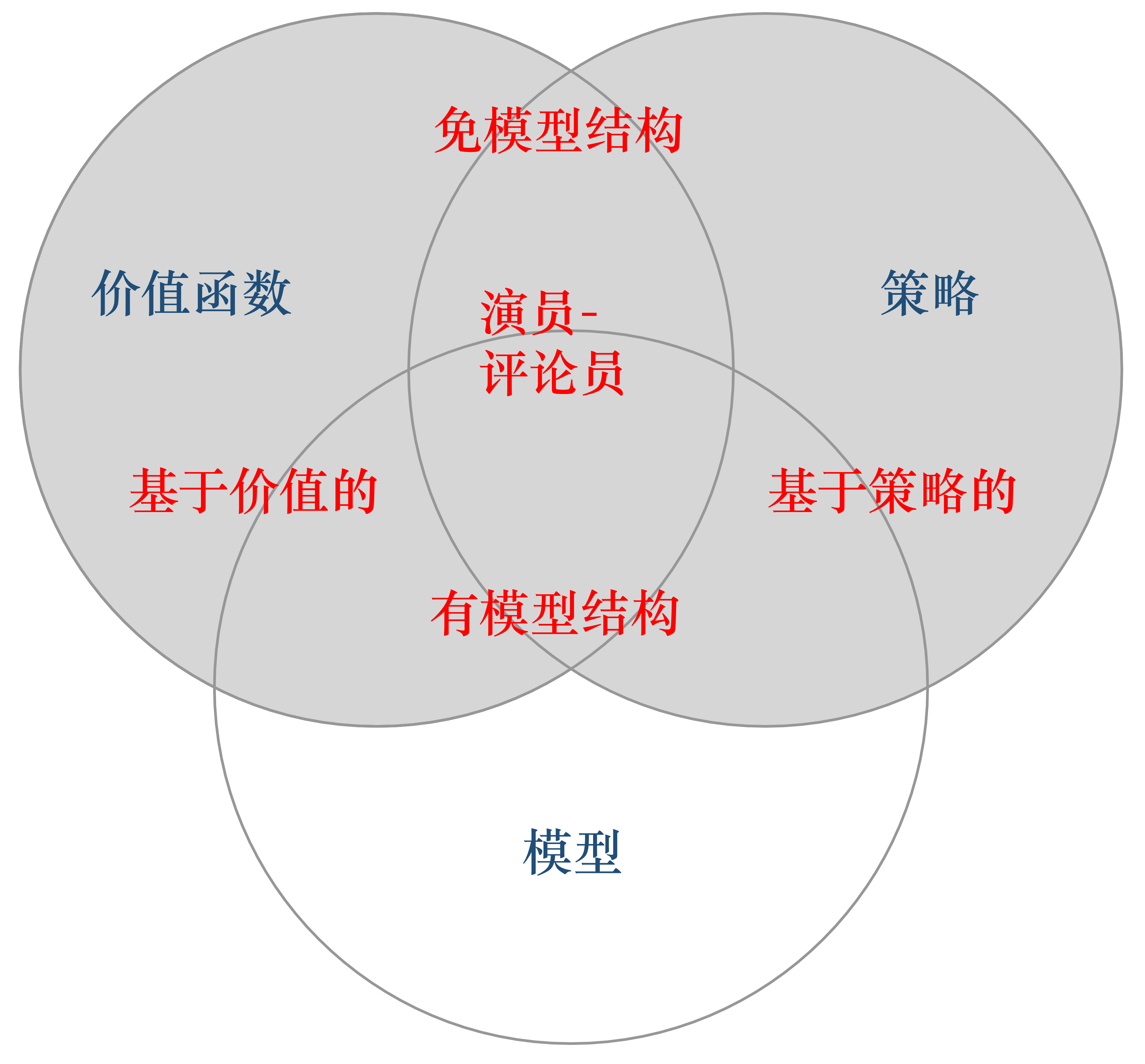
智能体类型¶
Question
基于策略和基于价值的强化学习方法有什么区别?
Answer
对于一个状态转移概率已知的马尔可夫决策过程,我们可以使用动态规划算法来求解。从决策方式来看,强化学习又可以划分为基于策略的方法和基于价值的方法。决策方式是智能体在给定状态下从动作集合中选择一个动作的依据,它是静态的,不随状态变化而变化。在基于策略的强化学习方法中,智能体会制定一套动作策略(确定在给定状态下需要采取何种动作),并根据这个策略进行操作。强化学习算法直接对策略进行优化,使制定的策略能够获得最大的奖励。而在基于价值的强化学习方法中,智能体不需要制定显式的策略,它维护一个价值表格或价值函数,并通过这个价值表格或价值函数来选取价值最大的动作。基于价值迭代的方法只能应用在不连续的、离散的环境下(如围棋或某些游戏领域),对于动作集合规模庞大、动作连续的场景(如机器人控制领域),其很难学习到较好的结果(此时基于策略迭代的方法能够根据设定的策略来选择连续的动作)。基于价值的强化学习算法有Q学习(Q-learning)、 Sarsa 等,而基于策略的强化学习算法有策略梯度(Policy Gradient,PG)算法等。此外,演员-评论员算法同时使用策略和价值评估来做出决策。其中,智能体会根据策略做出动作,而价值函数会对做出的动作给出价值,这样可以在原有的策略梯度算法的基础上加速学习过程,取得更好的效果。
Question
有模型强化学习和免模型强化学习有什么区别?
Answer
针对是否需要对真实环境建模,强化学习可以分为有模型强化学习和免模型强化学习。有模型强化学习是指根据环境中的经验,构建一个虚拟世界,同时在真实环境和虚拟世界中学习;免模型强化学习是指不对环境进行建模,直接与真实环境进行交互来学习到最优策略。
1.5 学习与规划¶
学习(learning)和规划(planning)是序列决策的两个基本问题
学习¶
在强化学习中,环境初始时是未知的,智能体不知道环境如何工作,它通过不断地与环境交互,逐渐改进策略。
规划¶
在规划中,环境是已知的,智能体被告知了(已经学习了)整个环境的运作规则的详细信息。智能体能够计算出一个完美的模型,并且在不需要与环境进行任何交互的时候进行计算。智能体不需要实时地与环境交互就能知道未来环境,只需要知道当前的状态,就能够开始思考,来寻找最优解。
范式¶
一个常用的强化学习问题解决思路是,先学习环境如何工作,也就是了解环境工作的方式,即学习得到一个模型,然后利用这个模型进行规划。
经典问题:K-臂赌博机¶
- 目标:通过有限次尝试最大化累积奖励。
- 策略:
- 仅探索:均匀尝试所有动作,精确估计奖励期望。
- 仅利用:始终选择当前最优动作,可能错过更高奖励动作。
- 平衡方法:ε-贪心、UCB(Upper Confidence Bound)等。
1.6 探索和利用¶
在强化学习里面,探索和利用是两个很核心的问题
- 探索:即我们去探索环境,通过尝试不同的动作来得到最佳的策略(带来最大奖励的策略)
- 利用:即我们不去尝试新的动作,而是采取已知的可以带来很大奖励的动作
刚开始的时候,强化学习智能体不知道它采取了某个动作后会发生什么,所以它只能通过试错去探索,所以探索就是通过试错来理解采取的动作到底可不可以带来好的奖励。利用是指我们直接采取已知的可以带来很好奖励的动作。所以这里就面临一个权衡问题,即怎么通过牺牲一些短期的奖励来理解动作,从而学习到更好的策略。
1.7 强化学习实验(Gym库)¶
环境搭建示例¶
import gym
env = gym.make("CartPole-v0") # 创建环境
observation = env.reset() # 初始化状态
for _ in range(1000):
action = env.action_space.sample() # 随机采样动作
observation, reward, done, info = env.step(action) # 执行动作
if done:
observation = env.reset() # 回合结束,重置环境
env.close()
代码说明:
-
gym.make() 创建经典控制问题CartPole环境。-
env.step(action) 返回四元组:新状态、即时奖励、终止标志、调试信息。 关键环境参数¶
| 环境 | 观测空间 | 动作空间 | 目标 |
|---|---|---|---|
| CartPole-v0 | 4维向量(位置、速度等) | 离散(左/右) | 保持杆直立尽可能久 |
| MountainCar-v0 | 2维向量(位置、速度) | 离散(左/右/不动) | 驱动小车到达山顶 |
1.8 关键词¶
-
强化学习(reinforcement learning,RL):智能体可以在与复杂且不确定的环境进行交互时,尝试使所获得的奖励最大化的算法。
-
动作(action): 环境接收到的智能体基于当前状态的输出。
-
状态(state):智能体从环境中获取的状态。
-
奖励(reward):智能体从环境中获取的反馈信号,这个信号指定了智能体在某一步采取了某个策略以后是否得到奖励,以及奖励的大小。
-
探索(exploration):在当前的情况下,继续尝试新的动作。其有可能得到更高的奖励,也有可能一无所有。
-
利用(exploitation):在当前的情况下,继续尝试已知的可以获得最大奖励的过程,即选择重复执行当前动作。
-
深度强化学习(deep reinforcement learning):不需要手动设计特征,仅需要输入状态就可以让系统直接输出动作的一个端到端(end-to-end)的强化学习方法。通常使用神经网络来拟合价值函数(value function)或者策略网络(policy network)。
-
全部可观测(full observability)、完全可观测(fully observed)和部分可观测(partially observed):当智能体的状态与环境的状态等价时,我们就称这个环境是全部可观测的;当智能体能够观察到环境的所有状态时,我们称这个环境是完全可观测的;一般智能体不能观察到环境的所有状态时,我们称这个环境是部分可观测的。
-
部分可观测马尔可夫决策过程(partially observable Markov decision process,POMDP):即马尔可夫决策过程的泛化。部分可观测马尔可夫决策过程依然具有马尔可夫性质,但是其假设智能体无法感知环境的状态,只能知道部分观测值。
-
动作空间(action space)、离散动作空间(discrete action space)和连续动作空间(continuous action space):在给定的环境中,有效动作的集合被称为动作空间,智能体的动作数量有限的动作空间称为离散动作空间,反之,则被称为连续动作空间。
-
基于策略的(policy-based):智能体会制定一套动作策略,即确定在给定状态下需要采取何种动作,并根据这个策略进行操作。强化学习算法直接对策略进行优化,使制定的策略能够获得最大的奖励。
-
基于价值的(valued-based):智能体不需要制定显式的策略,它维护一个价值表格或者价值函数,并通过这个价值表格或价值函数来执行使得价值最大化的动作。
-
有模型(model-based)结构:智能体通过学习状态的转移来进行决策。