Skip to content

约 3311 个字 12 张图片 预计阅读时间 17 分钟 共被读过 次

#RL

第3章 表格型方法总结

3.1 马尔可夫决策过程（MDP）

核心概念

  • 四元组：\((S, A, P, R)\)，分别表示状态集合、动作集合、状态转移概率、奖励函数。
  • 马尔可夫性质：下一时刻状态仅依赖当前状态和动作，不依赖历史。
  • 有模型 vs 免模型：
  • 有模型：已知\(P\)和\(R\)，可用动态规划（策略迭代、价值迭代）。
  • 免模型：未知\(P\)和\(R\)，依赖试错探索（如蒙特卡洛、时序差分）。

状态转移示例

\[ P(s_{t+1}, r_t | s_t, a_t) \]

表示在状态\(s_t\)执行动作\(a_t\)后转移到\(s_{t+1}\)并获得奖励\(r_t\)的概率。

3.2 Q表格

核心概念

  • Q函数：\(Q(s, a)\)表示在状态\(s\)选择动作\(a\)的长期期望回报。
  • Q表格：行代表状态，列代表动作，存储每个状态-动作对的Q值。
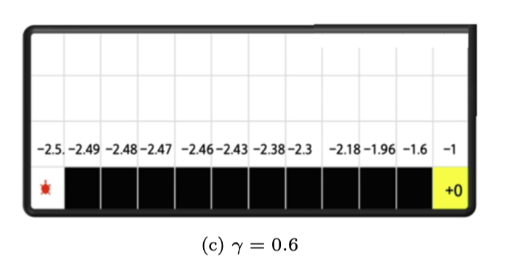
  • 折扣因子\(\gamma\)：平衡即时奖励与未来奖励的重要性（\(\gamma=0\)仅看单步，\(\gamma=1\)考虑无限步）。

示例：悬崖行走问题

  • 目标：从起点到终点，避免掉入悬崖。
  • 奖励：每走一步\(-1\)，掉崖\(-100\)。
  • Q值更新逻辑：
\[ G_t = r_{t+1} + \gamma G_{t+1} \quad (\text{从后往前递推}) \]

image.png

3.3 免模型预测

这些方法都是给定策略的！

方法对比

方法 更新方式 特点
蒙特卡洛 使用完整轨迹的回报均值更新Q值 高方差，需完整轨迹，无偏估计
时序差分 单步更新（TD目标 = 即时奖励 + γ·下一状态Q值） 低方差，可在线学习，有偏估计

蒙特卡洛(MC)更新公式

\[ V(s_t) \leftarrow V(s_t) + \alpha \left[ G_{t} - V(s_t) \right] \]
  • 其中， \(\alpha\) 代表的是学习率，可以人为设置
  • \(G_t\) 是把一条轨迹跑完后才得出来的回报

时序差分（TD）更新公式

\[ V(s_t) \leftarrow V(s_t) + \alpha \left[ r_{t+1} + \gamma V(s_{t+1}) - V(s_t) \right] \]
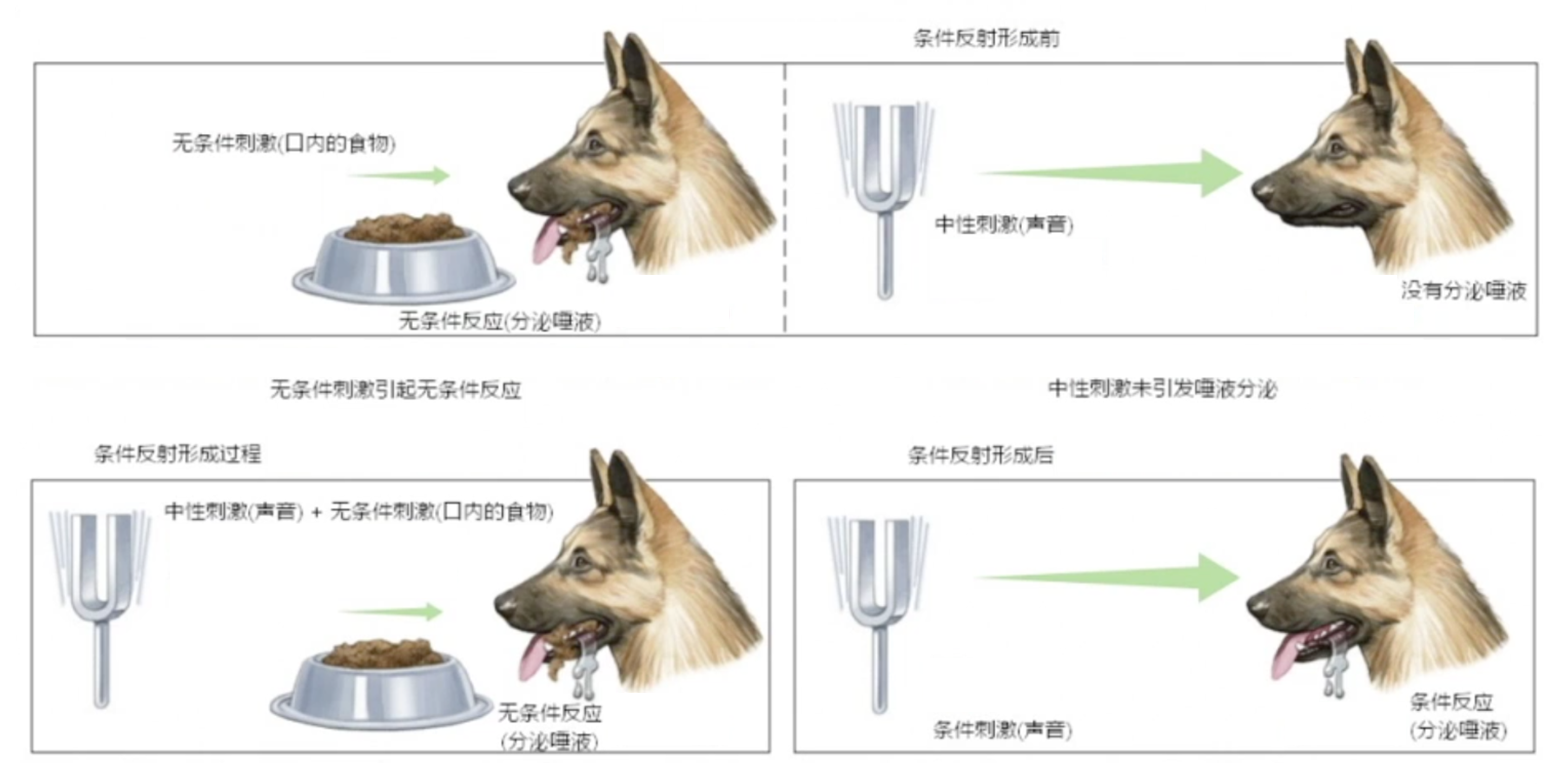
  • TD误差： \(\delta = r_{t+1} + \gamma V(s_{t+1}) - V(s_t)\) ，其中 \(\delta = r_{t+1} + \gamma V(s_{t+1})\) 被称为时序差分目标（TD target），时序差分目标是带衰减的未来奖励的总和。
  • 物理意义：类似巴甫洛夫条件反射，通过相邻状态的价值迭代更新。
    image.png

n步时序差分（n-step TD）

\[ \begin{align} n &= 1 (\text{TD}) &G_t^{(1)} = r_{t+1} + \gamma V(s_{t+1}) \\ n &= 2 &G_t^{(2)} = r_{t+1} + \gamma r_{t+2} + \gamma^2 V(s_{t+2}) \\ \vdots \\ n &= \infty \ (\text{MC}) &G_t^{\infty} = r_{t+1} + \gamma r_{t+2} + \cdots + \gamma^{T-t-1} r_T \end{align} \]

得到时序差分目标之后，我们用增量式学习（incremental learning）的方法来更新状态的价值：

\[ V(s_{t})←V(s_{t})+α(G_{t}^n−V(s_{t})) \]
  • 更新的深度与广度的对比一览图：
    image.png

3.4 免模型控制

我们不知道马尔可夫决策过程模型的情况下，如何优化价值函数，得到最佳的策略呢？我们可以把策略迭代进行广义的推广，使它能够兼容蒙特卡洛和时序差分的方法，即带有蒙特卡洛方法和时序差分方法的广义策略迭代（generalized policy iteration，GPI）。

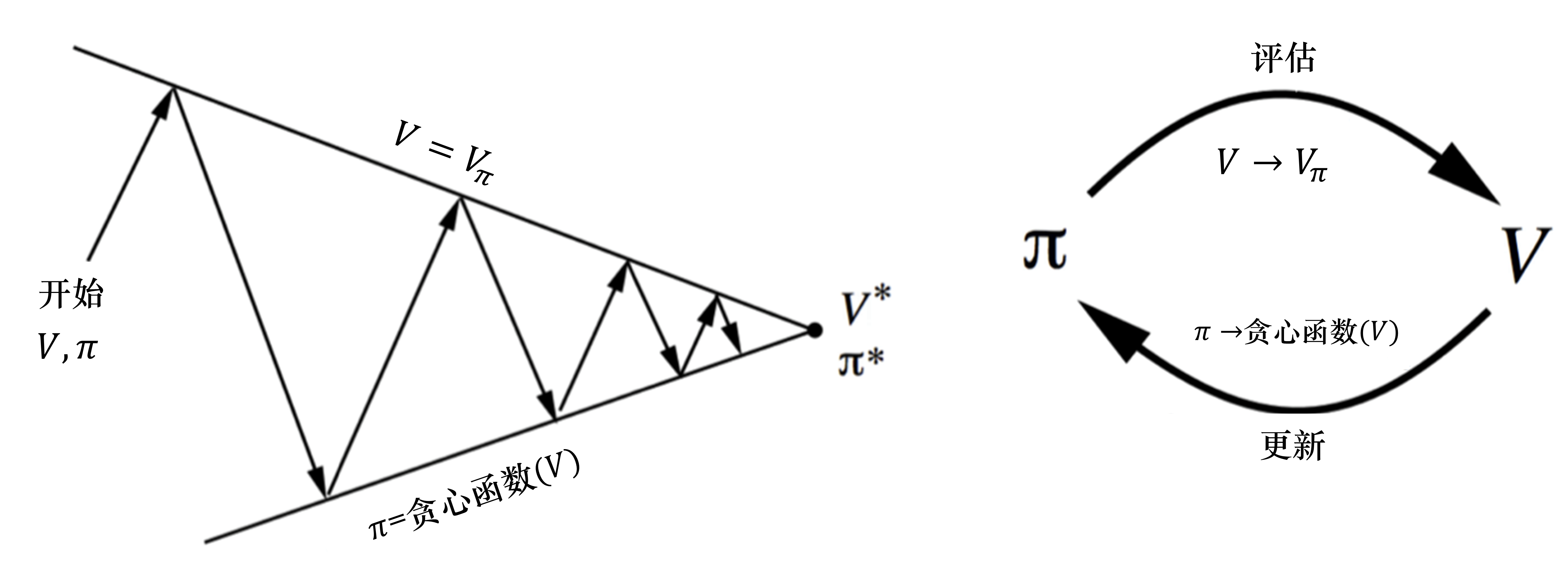
策略迭代由两个步骤组成。第一，我们根据给定的当前策略 \(\pi\) 来估计价值函数；第二，得到估计的价值函数后，我们通过贪心的方法来改进策略，即

\[ \pi^{'}=\text{贪心函数}(V_{\pi}) \]

这两个步骤是一个互相迭代的过程。

\[ \pi_{i+1}(s)=\underset{a}{\arg \max } Q_{\pi_{i}}(s, a) \]

我们可以计算出策略 \(\pi\) 的动作价值函数，并且可以计算针对状态 \(s \in S\) 的新策略 \(\pi_{i+1}\)。但得到状态价值函数后，我们并不知道奖励函数 \(R(s,a)\) 和状态转移 \(P(s'|s,a)\)，所以就无法估计 Q 函数

\[ Q_{\pi_{i}}(s, a)=R(s, a)+\gamma \sum_{s^{\prime} \in S} P\left(s^{\prime} \mid s, a\right) V_{\pi_{i}}\left(s^{\prime}\right) \]

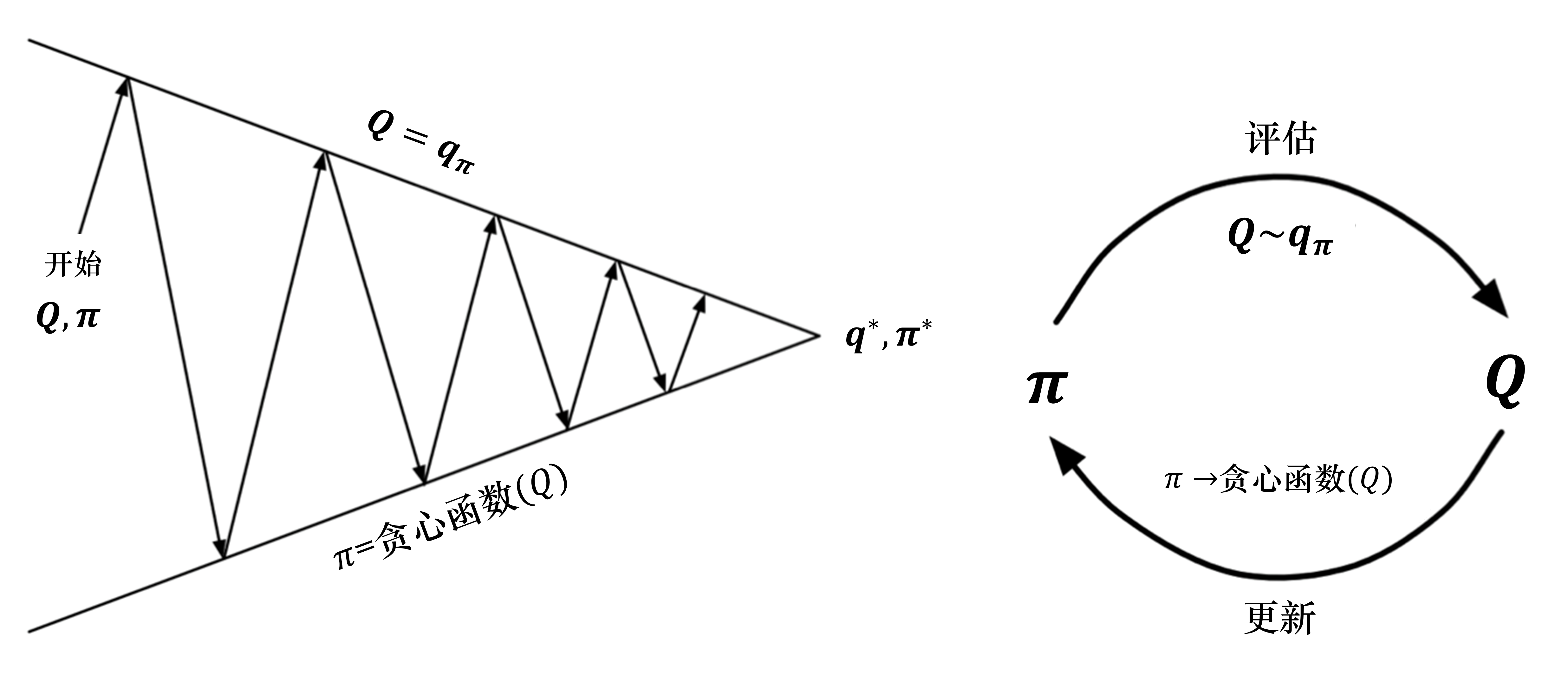
image.png
针对上述情况，我们引入了广义的策略迭代的方法。

我们对策略评估部分进行修改，使用蒙特卡洛的方法代替动态规划的方法估计 Q 函数。我们首先进行策略评估，使用蒙特卡洛方法来估计策略 \(Q=Q_{\pi}\)，然后进行策略更新，即得到 Q 函数后，我们就可以通过贪心的方法去改进它：

\[ \pi(s)=\underset{a}{\arg \max} Q(s, a) \]

image.png

一个保证策略迭代收敛的假设是回合有探索性开始（exploring start）。

假设每一个回合都有一个探索性开始，探索性开始保证所有的状态和动作都在无限步的执行后能被采样到，这样才能很好地进行估计。

算法通过蒙特卡洛方法产生很多轨迹，每条轨迹都可以算出它的价值。然后，我们可以通过平均的方法去估计 Q 函数。Q 函数可以看成一个Q表格，我们通过采样的方法把表格的每个单元的值都填上，然后使用策略改进来选取更好的策略。

如何用蒙特卡洛方法来填 Q 表格是这个算法的核心。
image.png
为了确保蒙特卡洛方法能够有足够的探索，我们使用了 \(\varepsilon\)-贪心（\(\varepsilon\text{-greedy}\)）探索。

\(\varepsilon\)-贪心是指我们有 \(1-\varepsilon\) 的概率会按照 Q函数来决定动作，通常 \(\varepsilon\) 就设一个很小的值， \(1-\varepsilon\) 可能是 0.9，也就是 0.9 的概率会按照Q函数来决定动作，但是我们有 0.1 的概率是随机的。通常在实现上，\(\varepsilon\) 的值会随着时间递减。在最开始的时候，因为我们还不知道哪个动作是比较好的，所以会花比较多的时间探索。接下来随着训练的次数越来越多，我们已经比较确定哪一个动作是比较好的，就会减少探索，把 \(\varepsilon\) 的值变小。主要根据 Q函数来决定动作，比较少随机决定动作，这就是 \(\varepsilon\)-贪心。

当我们使用蒙特卡洛方法和 \(\varepsilon\)-贪心探索的时候，可以确保价值函数是单调的、改进的。对于任何 \(\varepsilon\)-贪心策略 \(\pi\)，关于 \(Q_{\pi}\) 的 \(\varepsilon\)-贪心策略 \(\pi^{\prime}\) 都是一个改进，即 \(V_{\pi}(s) \leqslant V_{\pi^{\prime}}(s)\)，证明过程如下：

\[ \begin{aligned}     Q_{\pi}\left(s, \pi^{\prime}(s)\right) &=\sum_{a \in A} \pi^{\prime}(a \mid s) Q_{\pi}(s, a) \\     &=\frac{\varepsilon}{|A|} \sum_{a \in A} Q_{\pi}(s, a)+(1-\varepsilon) \max _{a} Q_{\pi}(s, a) \\     & \geqslant \frac{\varepsilon}{|A|} \sum_{a \in A} Q_{\pi}(s, a)+(1-\varepsilon) \sum_{a \in A} \frac{\pi(a \mid s)-\frac{\varepsilon}{|A|}}{1-\varepsilon} Q_{\pi}(s, a) \\     &=\sum_{a \in A} \pi(a \mid s) Q_{\pi}(s, a)=V_{\pi}(s)     \end{aligned} \]

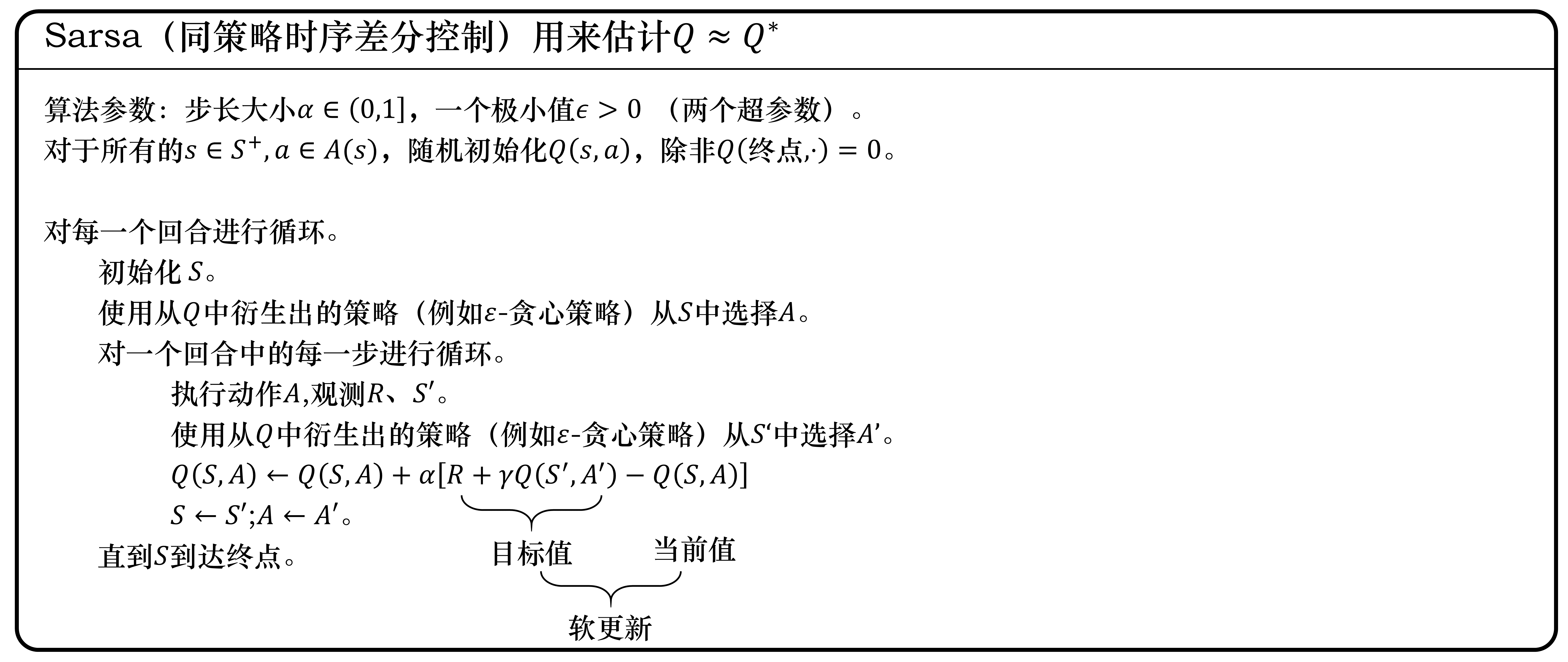
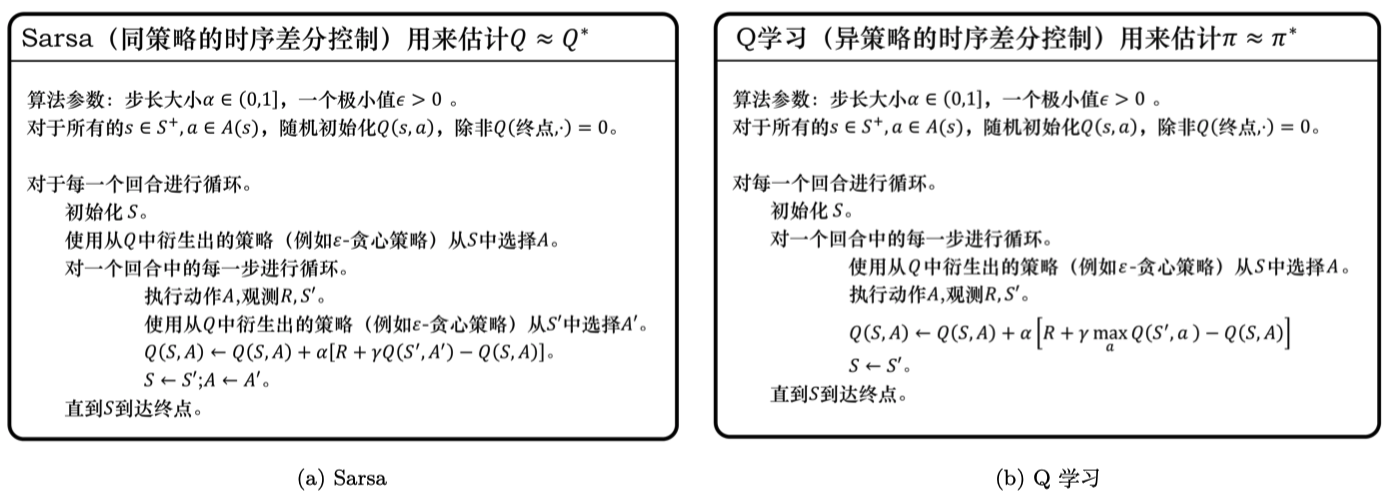
image.png

Sarsa（State-Action-Reward-State-Action同策略时序差分控制）

  • 更新规则：
\[ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}) - Q(s_t, a_t) \right] \]

image.png

  • 特点：使用实际执行的动作\(a_{t+1}\)更新Q值，策略保守，适合高风险环境（如悬崖行走）。
    image.png

Q学习（异策略）

  • 更新规则：
\[ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left[ r_{t+1} + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t) \right] \]

我们再通过对比的方式来进一步理解 Q学习。Q学习是异策略的时序差分学习方法，Sarsa 是同策略的时序差分学习方法。

Sarsa 在更新 Q 表格的时候，它用到的是 \(A'\) 。我们要获取下一个 Q 值的时候，\(A'\) 是下一个步骤一定会执行的动作，这个动作有可能是 \(\varepsilon\)-贪心方法采样出来的动作，也有可能是最大化 Q 值对应的动作，也有可能是随机动作，但这是它实际执行的动作。

但是 Q学习 在更新 Q 表格的时候，它用到的是 Q 值 \(Q(S',a)\) 对应的动作 ，它不一定是下一个步骤会执行的实际的动作，因为我们下一个实际会执行的那个动作可能会探索。

Q学习默认的下一个动作不是通过行为策略来选取的，Q学习直接看Q表格，取它的最大化的值，它是默认 \(A'\) 为最佳策略选取的动作，所以 Q学习 在学习的时候，不需要传入 \(A'\)，即 \(a_{t+1}\)  的值。
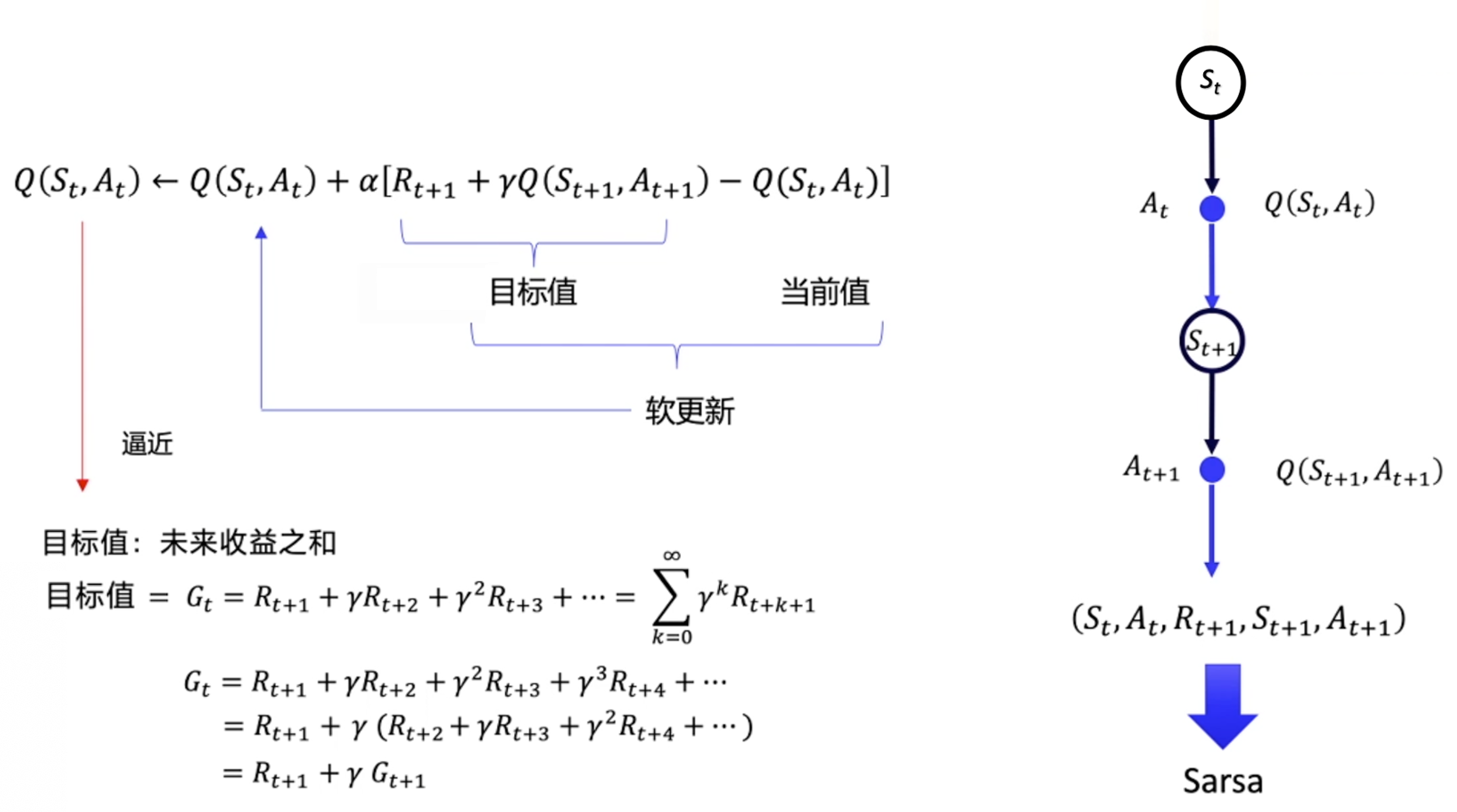
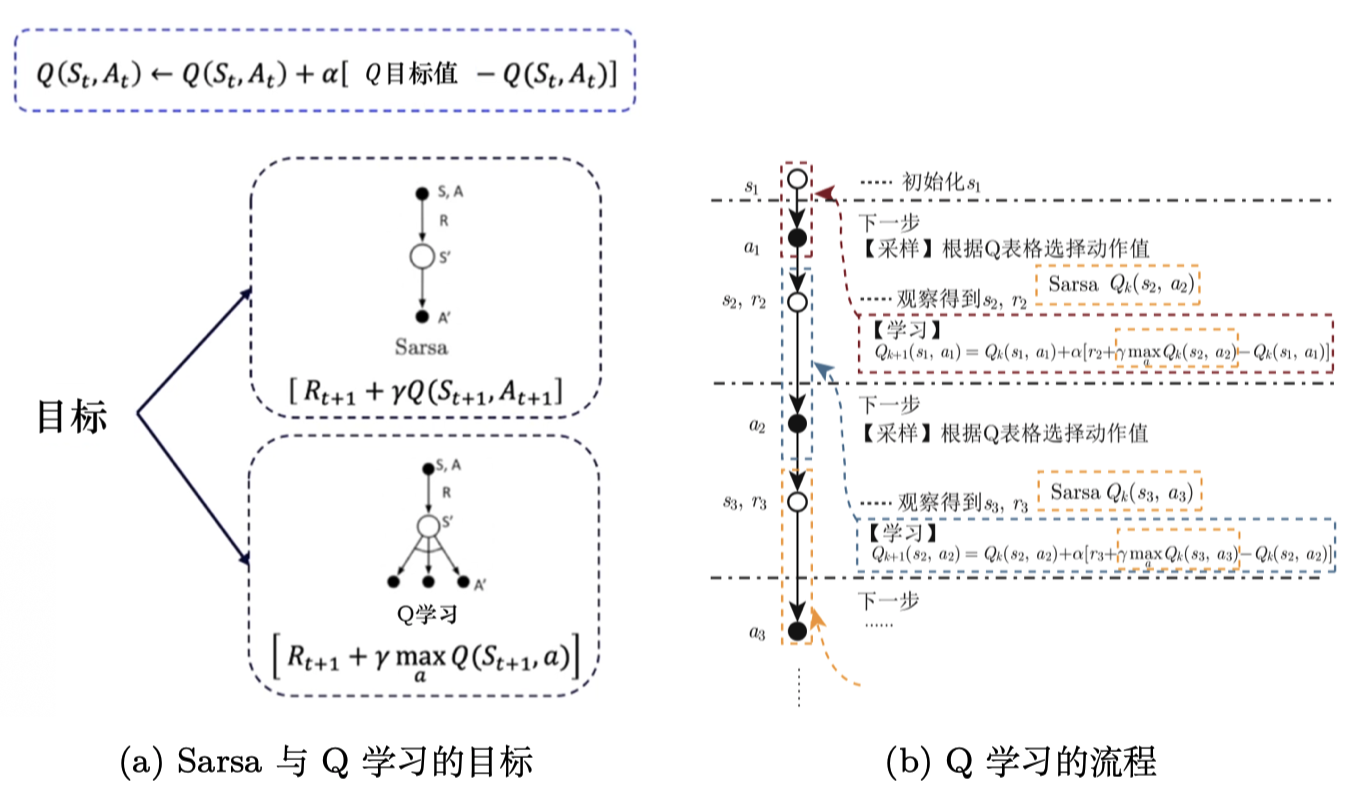
image.png

Sarsa 和 Q学习 的更新公式是一样的，区别只在目标计算的部分，
Sarsa 是 \(r_{t+1}+\gamma Q(s_{t+1}, a_{t+1})\)，
Q学习 是 \(r_{t+1}+\gamma  \underset{a}{\max} Q\left(s_{t+1}, a\right)\) 。

如图 3.34a 所示，Sarsa 用自己的策略产生了 \(S,A,R,S',A'\) 这条轨迹，然后用 \(Q(s_{t+1},a_{t+1})\) 去更新原本的 Q 值 \(Q(s_t,a_t)\)。
但是 Q学习 并不需要知道我们实际上选择哪一个动作 ，它默认下一个动作就是 Q 值最大的那个动作。Q学习知道实际上行为策略可能会有 0.1 的概率选择别的动作，但 Q 学习并不担心受到探索的影响，它默认按照最佳的策略去优化目标策略，所以它可以更大胆地去寻找最优的路径，它表现得比 Sarsa 大胆得多。

如图 3.34b 所示，我们对Q学习进行逐步拆解，Q学习与 Sarsa 唯一不一样的就是并不需要提前知道 \(A_2\) ，就能更新 \(Q(S_1,A_1)\) 。在一个回合的训练当中，Q学习 在学习之前也不需要获取下一个动作 \(A'\)，它只需要前面的 \((S,A,R,S')\) ，这与 Sarsa 很不一样。
image.png

同策略 vs 异策略

  • Sarsa 是一个典型的同策略算法，它只用了一个策略 \(\pi\)，它不仅使用策略 \(\pi\) 学习，还使用策略 \(\pi\) 与环境交互产生经验。如果策略采用 \(\varepsilon\)-贪心算法，它需要兼顾探索，为了兼顾探索和利用，它训练的时候会显得有点“胆小”。它在解决悬崖行走问题的时候，会尽可能地远离悬崖边，确保哪怕自己不小心探索了一点儿，也还是在安全区域内。此外，因为采用的是 \(\varepsilon\)-贪心 算法，策略会不断改变（\(\varepsilon\) 值会不断变小），所以策略不稳定。
  • Q学习是一个典型的异策略算法，它有两种策略————目标策略和行为策略，它分离了目标策略与行为策略。Q学习可以大胆地用行为策略探索得到的经验轨迹来优化目标策略，从而更有可能探索到最佳策略。行为策略可以采用 \(\varepsilon\)-贪心 算法，但目标策略采用的是贪心算法，它直接根据行为策略采集到的数据来采用最佳策略，所以 Q学习 不需要兼顾探索。
  • 我们比较一下 Q学习 和 Sarsa 的更新公式，就可以发现 Sarsa 并没有选取最大值的最大化操作。因此，Q学习是一个非常激进的方法，它希望每一步都获得最大的利益；Sarsa 则相对较为保守，它会选择一条相对安全的迭代路线。
    image.png

3.5 关键词

  • 概率函数和奖励函数：概率函数定量地表达状态转移的概率，其可以表现环境的随机性。但是实际上，我们经常处于一个未知的环境中，即概率函数和奖励函数是未知的。
  • Q表格：其表示形式是表格，其中表格的横轴为动作（智能体的动作），纵轴为环境的状态，每一个坐标点对应某时刻智能体和环境的状态，并通过对应的奖励反馈选择被执行的动作。一般情况下，Q表格是一个已经训练好的表格，不过我们也可以每执行一步，就对Q表格进行更新，然后用下一个状态的Q值来更新当前状态的Q值（即时序差分方法）。
  • 时序差分（temporal difference，TD）方法：一种Q函数（Q值）的更新方式，流程是使用下一步的Q值 \(Q(s_{t+1},a_{t+1})\) 来更新当前步的Q值 \(Q(s_t,a_t)\)。完整的计算公式如下：\(Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha [r_{t+1}+\gamma Q(s_{t+1},a_{t+1})-Q(s_t,a_t)]\) 。
  • Sarsa算法：一种更新前一时刻状态的单步更新的强化学习算法，也是一种同策略学习算法。该算法由于每次更新Q函数时需要知道前一步的状态、动作、奖励以及当前时刻的状态、将要执行的动作，即 \(s_{t}\)、\(a_{t}\)、\(r_{t+1}\)、\(s_{t+1}\)、\(a_{t+1}\) 这几个值，因此被称为 Sarsa 算法。智能体每进行一次循环，都会用 \(s_{t}\)、\(a_{t}\)、\(r_{t+1}\)、\(s_{t+1}\)、\(a_{t+1}\) 对前一步的Q值（函数）进行一次更新。