约 2982 个字 25 行代码 1 张图片 预计阅读时间 15 分钟 共被读过 次
近端策略优化(PPO)算法总结¶
5.1 重要性采样¶
核心概念¶
- 同策略与异策略:
- 同策略:智能体与环境交互并在此策略下进行更新。
- 异策略:训练时使用不同的策略进行数据采样,避免每次更新都需要重新交互。
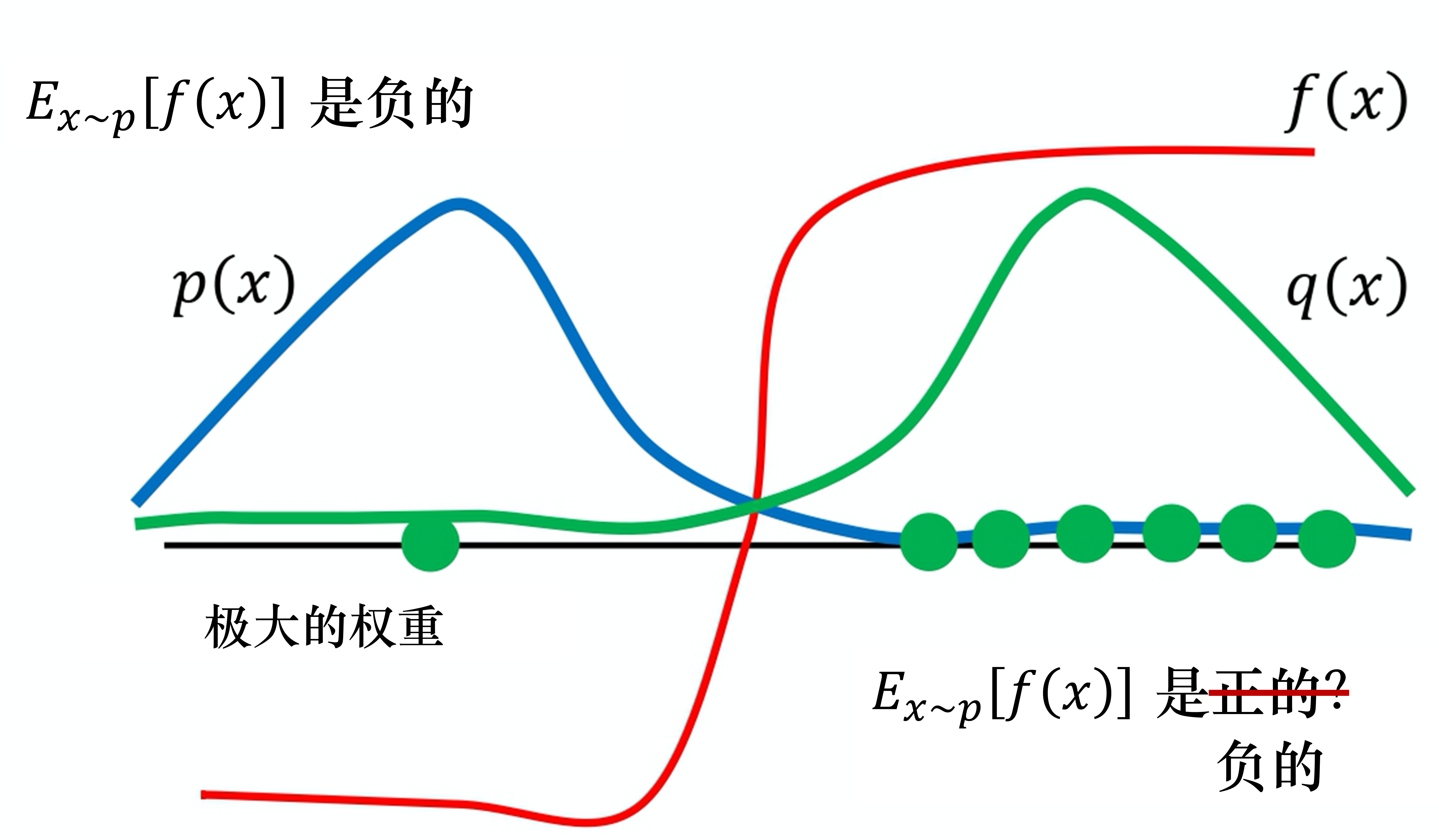
- 重要性采样:解决从异策略中采样数据的问题。通过引入重要性权重 \(\frac{p(x)}{q(x)}\),将一个策略的数据(\(q\))转换为另一个策略的数据(\(p\))。
公式¶
- 期望值计算:
- 如果可以从分布 \(p\) 采样数据,期望值为:
- 但如果只能从 \(q\) 采样,需加权修正为:
问题与限制¶
应用到异策略训练¶
- 异策略梯度更新:
- PPO通过异策略数据采样,结合重要性采样来更新策略参数。
- 核心公式为:
实际在做策略梯度的时候,我们并不是给整个轨迹 \(\tau\) 一样的分数,而是将每一个状态-动作对分开计算。实际更新梯度的过程可写为
我们用演员\(\theta\) 采样出 \(s_t\) 与 \(a_t\),采样出状态-动作的对,我们会计算这个状态-动作对的优势(advantage)\(A^{\theta}\left(s_{t}, a_{t}\right)\), 就是它有多好。\(A^{\theta}\left(s_{t}, a_{t}\right)\) 即用累积奖励减去基线,这一项就是估测出来的。它要估测的是,在状态 \(s_t\) 采取动作 \(a_t\) 是好的还是不好的。
我们可以通过重要性采样把同策略变成异策略,从 \(\theta\) 变成 \(\theta'\)。所以现在 \(s_t\)、\(a_t\) 是 \(\theta'\) 与环境交互以后所采样到的数据。 但是训练时,要调整的参数是模型 \(\theta\)。因为 \(\theta'\) 与 \(\theta\) 是不同的模型,所以我们要有一个修正的项。这个修正的项,就是用重要性采样的技术,把 \(s_t\)、\(a_t\) 用 \(\theta\) 采样出来的概率除以 \(s_t\)、\(a_t\) 用 \(\theta'\) 采样出来的概率。
接下来,我们可以拆解 \(p_{\theta}\left(s_{t}, a_{t}\right)\) 和 \(p_{\theta'}\left(s_{t}, a_{t}\right)\),即
$$
\begin{aligned}
p_{\theta}\left(s_{t}, a_{t}\right)&=p_{\theta}\left(a_{t}|s_{t}\right) p_{\theta}(s_t) \
p_{\theta'}\left(s_{t}, a_{t}\right)&=p_{\theta'}\left(a_{t}|s_{t}\right) p_{\theta'}(s_t)
\end{aligned}
$$
于是我们可得
这里需要做的一件事情是,假设模型是 \(\theta\) 的时候,我们看到 \(s_t\) 的概率,与模型是 \(\theta'\) 的时候,我们看到 \(s_t\) 的概率是一样的,即 \(p_{\theta}(s_t)=p_{\theta'}(s_t)\)。因为\(p_{\theta}(s_t)\)和\(p_{\theta'}(s_t)\)是一样的,所以我们可得
直接的理由就是 \(p_{\theta}(s_t)\) 很难算,\(p_{\theta}(s_t)\)有一个参数 \(\theta\),它表示的是我们用 \(\theta\) 去与环境交互,计算 \(s_t\) 出现的概率,而这个概率很难算。尤其是如果输入的是图片,同样的 \(s_t\) 可能根本就不会出现第二次。我们根本没有办法估计\(p_{\theta}(s_t)\),所以干脆就无视这个问题。
但是 \(p_{\theta}(a_t|s_t)\)很好算,我们有参数 \(\theta\) ,它就是一个策略网络。我们输入状态 \(s_t\) 到策略网络中,它会输出每一个 \(a_t\) 的概率。所以我们只要知道\(\theta\) 和 \(\theta'\) 的参数就可以计算 \(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)}\)。
我们可以从梯度反推原来的目标函数:
注意,对 \(\theta\) 求梯度时,\(p_{\theta^{\prime}}(a_{t} | s_{t})\) 和 \(A^{\theta^{\prime}}\left(s_{t}, a_{t}\right)\) 都是常数。
所以实际上,当我们使用重要性采样的时候,要去优化的目标函数为
我们将其记为 \(J^{\theta^{\prime}}(\theta)\),因为\(J^{\theta^{\prime}}(\theta)\) 括号里面的 \(\theta\) 代表我们要去优化的参数。\(\theta'\) 是指我们用 \(\theta'\) 做示范,就是现在真正在与环境交互的是 \(\theta'\)。因为 \(\theta\) 不与环境交互,是 \(\theta'\) 在与环境交互。然后我们用 \(\theta'\) 与环境交互,采样出 \(s_t\)、\(a_t\) 以后,要去计算 \(s_t\) 与 \(a_t\) 的优势 \(A^{\theta^{\prime}}\left(s_{t}, a_{t}\right)\),再用它乘 \(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)}\)。\(\frac{p_{\theta}\left(a_{t} | s_{t}\right)}{p_{\theta^{\prime}}\left(a_{t} | s_{t}\right)}\) 是容易计算的,我们可以从采样的结果来估测\(A^{\theta^{\prime}}\left(s_{t}, a_{t}\right)\) ,所以 \(J^{\theta^{\prime}}(\theta)\) 是可以计算的。
5.2 近端策略优化(PPO)¶
核心概念¶
- 目标函数与约束:PPO通过引入一个KL散度约束,限制训练中策略变动过大。
- 目标函数为:
TRPO与PPO的比较¶
- TRPO:信任区域策略优化,使用KL散度约束进行策略更新,优化困难。
- PPO:通过内置的KL散度约束简化了TRPO,使得实现更加高效。
KL散度与行为策略¶
- KL散度:度量两策略之间的行为差异(而非参数差异)。
- 行为策略:我们关注的是策略的行为差异,采用KL散度来度量两策略输出的动作分布差异。
5.2.1 近端策略优化惩罚(PPO-penalty)¶
- 通过增加KL散度惩罚项,避免策略变化过大,进行策略的多次更新。
- 目标函数为:
5.2.2 近端策略优化裁剪(PPO-clip)¶
- 通过对采样比值进行裁剪,确保模型更新不过度偏离上一策略。
- 裁剪后的目标函数为:
数学推导¶
重要性采样的推导¶
- 期望值计算:
- 假设我们希望计算从分布 \(p(x)\) 中采样得到的函数值的期望:
- 从分布 \(q(x)\) 采样时的修正:
- 当我们只能从分布 \(q(x)\) 采样数据时,可以使用重要性权重修正:
- 变换后的期望值公式:
- 期望值计算变为:
异策略更新中的梯度¶
- 同策略的梯度:
- 在策略梯度方法中,期望的梯度是基于同策略采样的:
- 异策略的梯度:
- 当使用异策略时,我们需要加上重要性权重进行修正:
PPO的目标函数推导¶
- 优化目标:
- PPO的目标函数通过在原目标函数中加入KL散度约束来优化:
- TRPO与PPO的区别:
- TRPO:KL散度作为约束存在于目标函数外部,需要优化时处理复杂约束:
- PPO:KL散度作为约束直接加入目标函数,简化优化过程:
- KL散度的解释:
- KL散度用于衡量两个策略在行为上的差异,即给定状态下两个策略输出的动作分布的差异。
- 行为差异:在强化学习中,我们关心的是策略在执行时的行为差异,而非参数差异。
PPO的变种¶
- PPO-penalty:通过KL散度惩罚来限制策略变化过大,并在每个训练迭代中多次更新参数。
- PPO-clip:通过裁剪操作来确保策略更新不会偏离太远。其目标函数为:
关键对比与总结¶
| 特性 | PPO-Penalty | PPO-Clip |
|---|---|---|
| 约束方式 | KL 散度惩罚项 | 策略比率裁剪 |
| 调参复杂度 | 需动态调整 \(\beta\) | 固定 \(\epsilon\) |
| 计算开销 | 需计算 KL 散度 | 无需额外分布计算 |
| 适用场景 | 高精度策略更新 | 快速训练与简化实现 |
关键词¶
- 同策略(on-policy):要学习的智能体和与环境交互的智能体是同一个时对应的策略。
- 异策略(off-policy):要学习的智能体和与环境交互的智能体不是同一个时对应的策略。
- 重要性采样(important sampling):使用另外一种分布,来逼近所求分布的一种方法,在强化学习中通常和蒙特卡洛方法结合使用,公式如下:
我们在已知 \(q\) 的分布后,可以使用上式计算出从 \(p\) 这个分布采样 \(x\) 代入 \(f\) 以后得到的期望值。
- 近端策略优化(proximal policy optimization,PPO):避免在使用重要性采样时由于在 \(\theta\) 下的 \(p_{\theta}\left(a_{t} | s_{t}\right)\) 与在 \(\theta '\) 下的 \(p_{\theta'}\left(a_{t} | s_{t}\right)\) 相差太多,导致重要性采样结果偏差较大而采取的算法。具体来说就是在训练的过程中增加一个限制,这个限制对应 \(\theta\) 和 \(\theta'\) 输出的动作的KL散度,来衡量 \(\theta\) 与 \(\theta'\) 的相似程度。
PPO 训练细节¶
- 注意
.detach(),不需要的梯度记得.detach(),并且.detach()后对该对象之后的计算图的计算没有影响 - 注意损失函数
self.entropy_coef * dist.entropy().mean(),符号为正,最后的策略更确定,符号为负,最后的策略更随机
核心代码:
for _ in range(self.k_epochs):
# compute advantage
values = self.critic(old_states) # detach to avoid backprop through the critic
advantage = returns - values.detach()
# get action probabilities
probs = self.actor(old_states)
dist = Categorical(probs)
# get new action probabilities
new_probs = dist.log_prob(old_actions)
# compute ratio (pi_theta / pi_theta__old):
ratio = torch.exp(new_probs - old_log_probs) # old_log_probs must be detached
# compute surrogate loss
surr1 = ratio * advantage
surr2 = torch.clamp(ratio, 1 - self.eps_clip, 1 + self.eps_clip) * advantage
# compute actor loss
actor_loss = -torch.min(surr1, surr2).mean() + self.entropy_coef * dist.entropy().mean()
# compute critic loss
critic_loss = (returns - values).pow(2).mean()
# take gradient step
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
actor_loss.backward()
critic_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()