约 1812 个字 103 行代码 1 张图片预计阅读时间 10 分钟共被读过次

#RL #DQN

第7章深度Q网络进阶技巧¶

7.1 双深度Q网络（Double DQN, DDQN）¶

关键概念¶

问题：Q值高估。传统DQN在计算目标值时直接使用目标网络的最大Q值，导致高估。
分析：例如，假设我们现在有 4 个动作，本来它们得到的Q值都是差不多的，它们得到的奖励也是差不多的。但是在估计的时候，网络是有误差的。所示，假设是第一个动作被高估了，绿色代表是被高估的量，智能体就会选这个动作，就会选这个高估的 Q 值来加上 \(r_t\) 来当作目标。如果第四个动作被高估了，智能体就会选第四个动作来加上 \(r_t\) 当作目标。所以智能体总是会选那个 Q 值被高估的动作，总是会选奖励被高估的动作的Q值当作最大的结果去加上 \(r_t\) 当作目标，所以目标值总是太大。
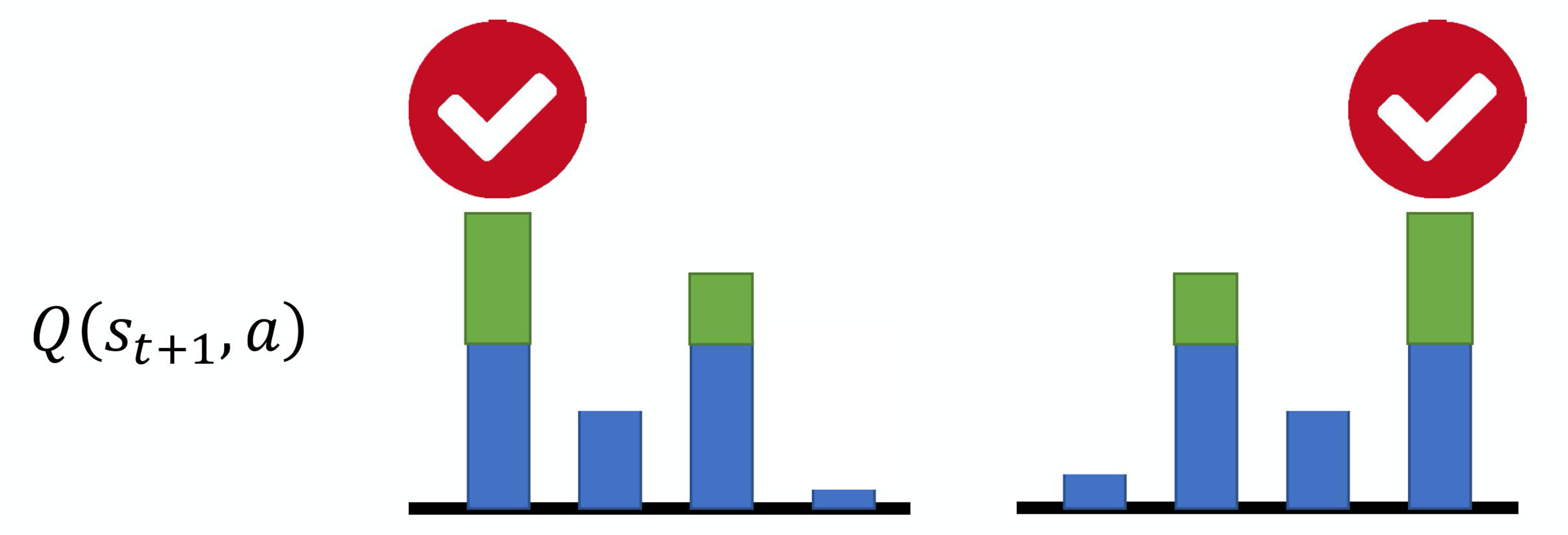
解决方案：分离动作选择和值计算：
用当前网络选择动作：\(a^* = \arg\max_a Q(s_{t+1}, a)\)
用目标网络计算值：\(Q'(s_{t+1}, a^*)\)

数学公式¶

传统DQN目标：

\[ Q(s_t, a_t) \leftrightarrow r_t + \max_a Q'(s_{t+1}, a) \tag{7.1} \]

DDQN目标：

\[ Q(s_t, a_t) \leftrightarrow r_t + Q'\left(s_{t+1}, \arg\max_a Q(s_{t+1}, a)\right) \tag{7.2} \]

实现细节¶

使用两个网络：当前网络（频繁更新）和目标网络（定期同步）。
改动少，计算量与DQN相当。

关键代码¶

Python

        state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(
            self.batch_size)
        # 将数据转换为tensor
        state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
        action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)  
        reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float).unsqueeze(1)    
        next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
        done_batch = torch.tensor(np.float32(done_batch), device=self.device).unsqueeze(1)
        q_value_batch = self.policy_net(state_batch).gather(dim=1, index=action_batch) # 实际的Q值
        
        next_q_value_batch = self.policy_net(next_state_batch) # 下一个状态对应的实际策略网络Q值
        next_target_value_batch = self.target_net(next_state_batch) # 下一个状态对应的目标网络Q值
        # 将策略网络Q值最大的动作对应的目标网络Q值作为期望的Q值
        next_target_q_value_batch = next_target_value_batch.gather(1, torch.max(next_q_value_batch, 1)[1].unsqueeze(1))
        expected_q_value_batch = reward_batch + self.gamma * next_target_q_value_batch* (1-done_batch) # 期望的Q值
        """dqn版本
    next_q_value_batch = self.target_net(next_state_batch).max(1)[0].detach() # 计算下一时刻的状态(s_t_,a)对应的Q值
        # 计算期望的Q值，对于终止状态，此时done_batch[0]=1, 对应的expected_q_value等于reward
        next_target_value_batch = reward_batch + self.gamma * next_q_values * (1-done_batch)
    """

        # 计算损失
        loss = nn.MSELoss()(q_value_batch, expected_q_value_batch)

7.2 竞争深度Q网络（Dueling DQN）¶

网络结构改进¶

将Q网络分解为两条路径：
状态值函数 \(V(s)\)：标量，表示状态的价值。
优势函数 \(A(s, a)\)：向量，表示动作的相对优势。

数学公式¶

\[ Q(s, a) = V(s) + A(s, a) \]

think

由于一个动作而更新 V 的同时，会将其余的Q（s, a）一起更新

约束条件¶

零均值化：强制优势函数的每列和为0，避免\(V(s)\)与\(A(s, a)\)冗余。

Python

# 零均值化伪代码
advantages = A(s, a) - mean(A(s, a))
Q = V(s) + advantages

优势¶

数据效率高：更新\(V(s)\)可间接影响所有动作的Q值。
示例：若需提升某动作Q值，可能仅需调整\(V(s)\)。

关键代码¶

Python

#### 主要是模型上的差别
class DuelingNet(nn.Module):
    def __init__(self, n_states, n_actions,hidden_dim=128):
        super(DuelingNet, self).__init__()
        # hidden layer
        self.hidden_layer = nn.Sequential(
            nn.Linear(n_states, hidden_dim),
            nn.ReLU()
        )
        #  advantage
        self.advantage_layer = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, n_actions)
        )
        # value
        self.value_layer = nn.Sequential(
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, 1)
        )
    def forward(self, state):
        x = self.hidden_layer(state)
        advantage = self.advantage_layer(x)
        value     = self.value_layer(x)
        return value + advantage - advantage.mean()

7.3 优先级经验回放（Prioritized Experience Replay, PER）¶

核心思想¶

非均匀采样：根据时序差分误差（TD error）赋予经验优先级。
高TD误差的经验更可能被采样。

实现步骤¶

计算经验优先级：\(p_i = |\delta_i| + \epsilon\)（\(\delta_i\)为TD误差）。
按优先级概率采样：\(P(i) = \frac{p_i^\alpha}{\sum_j p_j^\alpha}\)。
重要性采样调整更新权重。

7.4 多步方法（平衡MC与TD）¶

核心思想¶

混合蒙特卡洛（MC）与时序差分（TD）：使用\(N\)步奖励。
目标值计算：

\[ \text{目标} = \sum_{t'=t}^{t+N} r_{t'} + \gamma^N \max_a Q(s_{t+N+1}, a) \]

优缺点¶

优点：减少Q值估计偏差。
缺点：增加奖励方差。

7.5 噪声网络（Noisy Net）¶

改进探索¶

参数空间加噪声：在Q网络参数上添加高斯噪声。
回合内噪声固定，实现状态依赖的探索。

实现方式¶

每回合开始时采样噪声，保持回合内参数不变。
动作选择：\(a = \arg\max_a \tilde{Q}(s, a)\)（\(\tilde{Q}\)为噪声Q网络）。

核心代码¶

Python

class NoisyLinear(nn.Module):
    def __init__(self, input_dim, output_dim, std_init=0.4):
        super(NoisyLinear, self).__init__()
        self.input_dim  = input_dim
        self.output_dim = output_dim
        self.std_init     = std_init
        self.weight_mu    = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
        self.weight_sigma = nn.Parameter(torch.FloatTensor(output_dim, input_dim))
        self.register_buffer('weight_epsilon', torch.FloatTensor(output_dim, input_dim))
        self.bias_mu    = nn.Parameter(torch.FloatTensor(output_dim))
        self.bias_sigma = nn.Parameter(torch.FloatTensor(output_dim))
        self.register_buffer('bias_epsilon', torch.FloatTensor(output_dim))
        self.reset_parameters()
        self.reset_noise()
    def forward(self, x):
        if self.training:
            weight = self.weight_mu + self.weight_sigma.mul(torch.tensor(self.weight_epsilon))
            bias   = self.bias_mu   + self.bias_sigma.mul(torch.tensor(self.bias_epsilon))
        else:
            weight = self.weight_mu
            bias   = self.bias_mu
        return F.linear(x, weight, bias)
    def reset_parameters(self):
        mu_range = 1 / math.sqrt(self.weight_mu.size(1))
        self.weight_mu.data.uniform_(-mu_range, mu_range)
        self.weight_sigma.data.fill_(self.std_init / math.sqrt(self.weight_sigma.size(1)))
        self.bias_mu.data.uniform_(-mu_range, mu_range)
        self.bias_sigma.data.fill_(self.std_init / math.sqrt(self.bias_sigma.size(0)))
    def reset_noise(self):
        epsilon_in  = self._scale_noise(self.input_dim)
        epsilon_out = self._scale_noise(self.output_dim)
        self.weight_epsilon.copy_(epsilon_out.ger(epsilon_in))
        self.bias_epsilon.copy_(self._scale_noise(self.output_dim))
    def _scale_noise(self, size):
        x = torch.randn(size)
        x = x.sign().mul(x.abs().sqrt())
        return x
class NoisyMLP(nn.Module):
    def __init__(self, input_dim,output_dim,hidden_dim=128):
        super(NoisyMLP, self).__init__()
        self.fc1 =  nn.Linear(input_dim, hidden_dim)
        self.noisy_fc2 = NoisyLinear(hidden_dim, hidden_dim)
        self.noisy_fc3 = NoisyLinear(hidden_dim, output_dim)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.noisy_fc2(x))
        x = self.noisy_fc3(x)
        return x
    def reset_noise(self):
        self.noisy_fc2.reset_noise()
        self.noisy_fc3.reset_noise()

7.6 分布式Q函数（Distributional Q-function）¶

核心思想¶

建模奖励分布：输出奖励的概率分布而非期望值。
示例：将奖励范围离散化为\([-10, 10]\)，预测每个区间的概率。

网络输出¶

每个动作对应一个分布向量（如5个区间概率）。
测试时选择均值最大的动作。

优势¶

捕捉奖励不确定性，支持风险敏感策略。

7.7 彩虹（Rainbow）¶

方法整合¶

7种技术组合：DDQN、Dueling DQN、PER、多步、噪声网络、分布式Q函数、竞争架构。
性能对比（图7.10）：
彩虹方法（彩色实线）显著优于单一方法。
去除多步或分布式Q函数性能下降明显（图7.11）。

关键结论¶

分布式Q函数天然缓解高估问题，使DDQN作用减弱。
多步方法对性能影响最大。

关键词¶

双深度Q网络（double DQN）：在双深度Q网络中存在两个Q网络，第一个Q网络决定哪一个动作的Q值最大，从而决定对应的动作。另一方面，Q值是用 \(Q'\) 计算得到的，这样就可以避免过度估计的问题。具体地，假设我们有两个Q函数并且第一个Q函数高估了它现在执行的动作 \(a\) 的值，这没关系，只要第二个Q函数 \(Q'\) 没有高估动作 \(a\) 的值，那么计算得到的就还是正常的值。
竞争深度Q网络（dueling DQN）：将原来的深度Q网络的计算过程分为两步。第一步计算一个与输入有关的标量 \(\mathrm{V(s)}\)；第二步计算一个向量 \(\mathrm{A(s,a)}\) 对应每一个动作。最后的网络将两步的结果相加，得到我们最终需要的Q值。用一个公式表示就是 \(\mathrm{Q(s,a)=V(s)+A(s,a)}\) 。另外，竞争深度Q网络，使用状态价值函数与动作价值函数来评估Q值。
优先级经验回放（prioritized experience replay，PER）：这个方法是为了解决我们在第6章中提出的经验回放方法的不足而提出的。我们在使用经验回放时，均匀地取出回放缓冲区（reply buffer）中的采样数据，这里并没有考虑数据间的权重大小。但是我们应该将那些训练效果不好的数据对应的权重加大，即其应该有更大的概率被采样到。综上，优先级经验回放不仅改变了被采样数据的分布，还改变了训练过程。
噪声网络（noisy net）：其在每一个回合开始的时候，即智能体要和环境交互的时候，在原来的Q函数的每一个参数上加上一个高斯噪声（Gaussian noise），把原来的Q函数变成 \(\tilde{Q}\) ，即噪声Q函数。同样，我们把每一个网络的权重等参数都加上一个高斯噪声，就得到一个新的网络 \(\tilde{Q}\) 。我们会使用这个新的网络与环境交互直到结束。
分布式Q函数（distributional Q-function）：对深度Q网络进行模型分布，将最终网络的输出的每一类别的动作再进行分布操作。
彩虹（rainbow）：将7个技巧/算法综合起来的方法，7个技巧分别是——深度Q网络、双深度Q网络、优先级经验回放的双深度Q网络、竞争深度Q网络、异步优势演员-评论员算法（A3C）、分布式Q函数、噪声网络，进而考察每一个技巧的贡献度或者与环境的交互是否是正反馈的。