第8章 针对连续动作的深度Q网络总结¶

深度Q网络与策略梯度的比较¶

• 深度Q网络比策略梯度更稳定
• 深度Q网络容易训练的原因：
  • 只要能估计出Q函数，就能找到好的策略
  • 估计Q函数是回归问题，易于评估（通过损失函数下降）
  • 策略的改进有保证

深度Q网络的主要挑战：连续动作¶

连续动作的应用场景¶

• 控制方向盘角度（自动驾驶）
• 控制机器人多个关节角度（机器人控制）

连续动作的挑战¶

• 深度Q网络需要解决的核心优化问题：

  Text Only

  a = argmax_a Q(s,a)
  

• 离散动作易于穷举所有可能性

• 连续动作无法枚举所有可能值

解决连续动作的四种方案¶

方案1：对动作进行采样¶

• 采样N个可能的动作：{a₁, a₂, ..., aₙ}
• 利用GPU并行计算这N个动作的Q值
• 选择Q值最大的动作
• 缺点：采样有限，结果可能不精确

方案2：梯度上升¶

• 将a作为参数，用梯度上升更新a的值
• 目标是最大化Q函数
• 缺点：
  • 可能找到局部最大值而非全局最大值
  • 计算成本高（每次决策都需要迭代训练）

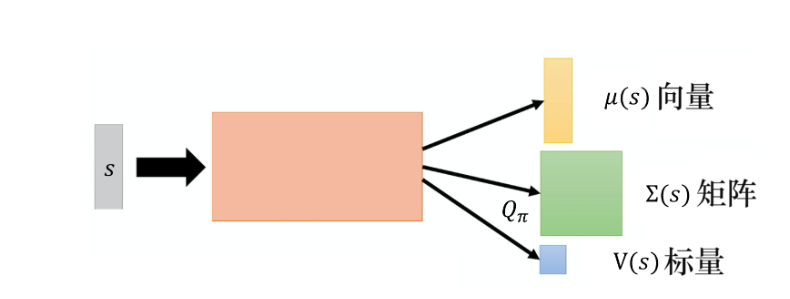
方案3：特殊设计网络架构¶

[1603.00748] Continuous Deep Q-Learning with Model-based Acceleration

• 设计特殊的Q函数形式，使argmax操作变得简单

• 网络架构：

  • 输入状态s
  • 输出：向量μ(s)、矩阵Σ(s)和标量V(s)
  • Q函数设计为：

  $$

Q(s,a)=-(a-\mu(s))^T \Sigma(s)(a-\mu(s))+V(s)

$$
- 其中Σ(s)是正定矩阵，通过Σ(s)=LL^T构造，L为下三角矩阵
- 求解argmax:

- 要最大化Q(s,a)，需要最小化$(a-\mu(s))^T \Sigma(s)(a-\mu(s))$
- 当a=μ(s)时，该项为0，达到最小
- 因此最优动作a=μ(s)

方案4：不使用深度Q网络¶

• 将基于策略的方法(PPO)和基于价值的方法(DQN)结合
• 采用演员-评论员架构

关键概念¶

连续动作空间¶

• 动作表示为向量，每个维度可以取连续值
• 例如：机器人控制中，向量各维度表示不同关节角度

正定矩阵¶

• n阶对称矩阵A，满足对任意非零n维向量x，都有x^T·A·x>0
• 在方案3中用于构造特殊的Q函数形式

argmax操作¶

• 深度Q网络的核心挑战
• 在连续动作空间中难以直接求解